RSA algorithm is quite easy to implement. It’s been around since 1979 and it is still quite safe.
We only need two prime numbers p and q. Let’s imagine p=701 and q=997.
The way to test a number is a prime number could be like this one: k**(p-1)%p = 1. Being k a natural integer (let’s say 2) and p a prime number. So, in my case and using Python interpreter:
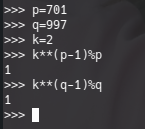
After we have the prime number, we need to evaluate the “modulus” number. It is p*q = 701*997 = 698897. Let’s call this number n — n=698897.
Once we have the modulus, we can calculate the Euler’s Totient function for n. Which, given that p and q are prime numbers and n is p*q, eu(n)=(p-1)(q-1) = 102 * 232 = 697200.
We only need to choose a number coprime with 697200. Let’s call this number e and ramdomly I’ll choose e=179. This number e will be used as the public key.
Only one more thing is needed: our private key. The private key will be a number d satisfying e*d%eu(n) == 1. This is only possible if e and n are coprime numbers. So, lets say d=140219.
e*d%eu(n) = 1 — I mean (179*140219)%697200 = 1
So the d is my private key. You should never share your private key. Never!
An use case
Let’s imagine I have my credit card and my mobile phone with me. But I don’t remember the code for my credit card and I can’t use it. So I ask my wife using a message in the mobile phone. “Please, can you tell me the number of the credit card? Please, encode it using RSA with public key 179 and modulus 698897. Thank you, dear”
Now let’s imagine that the credit card code is 5237.
My wife will do the following calculation: 5237**e%n = 197497
And she can answer the message like this: “The code is 197497”.
Great, now I know that the credit card code is 197497**d%n = 5237 — I can use my credit card now!!!!
However, someone steals my phone and my credit card. NOOOOOO!!!!! And the theft is able to see the messages and he knows that the public key is 179 and the modulus is 140219. However, he needs to find out what is private key. The private key is not in the messages.
Finding out the private key from the public key.
Well… the theft have the modulus (698897) and also the public key 179. And he also knows the secret message is “197497”.
So, he needs to find 2 prime numbers p,q so that n=p*q. For sure he knows that 1 and 2 are not these numbers, and he knows that the smallest number in (p,q) will be smaller or equal to the squared root of n. And none of them will be an even number..
So, for sure he could guess the private key finding out p,q. This can easily be done using this silly python script:
for np in range(3,ceil(sqrt(n)), 2):
if (n%np==0):
nq = n/np
print(np, nq)
breakSo he can easily find out what were the p and q values: 701 and 997. So he can find out the value of the Euler Toitient function: eun=(700*996) = 697200
And knowing that e=179 he can just find out the private key value using the following python script (the next algorithm is not efficient at all, but it is enough in this case for the sake of simplicity):
for d in range(1,eun):
if (e*d%eun==1):
print(d)
break
After running that, the theft knows that d is 140219. He guessed the Private Key value. The only thing he has left to do to guess the decrypted message: 197497**d%n = 5237
The theft got it!!! 5237 is code for the card. He can steal the money and this was done in very little time.
So RSA is a weak Cryptographic System.
Well, I wouldn’t consider that to be true. I’ve just used a 20bit modulus. So the algorithm finds the solution in 725 steps as maximum: ceil(sqrt(2**20-1)/2)
If I used 768 bit modulus (which is considered to be really unsecure) the algorithm would only need 27861425773824902618883922777920627422247679544911070145715529933961303512072360206822627414227418267832271612411904 steps as maximum to find out a reliable solution. This has been accomplished in only 22.5 hours.
Given that the least recommended is 2048 bits, and that it is recommended 4096 bits you can imagine that reliably finding out the numbers could take as long as 2.612e1232 steps to find out the solution as maximum. Quite a bit hard to evaluate that!!!
